Uji t adalah salah satu instrumen statistik untuk menentukan rata-rata dari sekumpulan kelompok apakah berbeda secara signifikan dengan sekumpulan rata-rata pada kelompok lainnya. Para praktisi laboratorium baik di level Penyelia atau Manajer Teknis bahkan Manajer Mutu, sering menggunakan uji t untuk menentukan suatu evaluasi.
Evaluasi tersebut diantaranya pada saat validasi metode uji, uji profisiensi laboratorium dan cek antara peralatan gelas atau instrumen. Oleh sebab itu, kami ingin memberikan informasi mengenai definisi dan cara menghitung menggunakan rumus uji t.


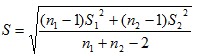




Ok, demikian dulu sekilat pembahasan dari labmutu mengenai salah satu uji statistik yang cukup populer ini. Terimakasih
Evaluasi tersebut diantaranya pada saat validasi metode uji, uji profisiensi laboratorium dan cek antara peralatan gelas atau instrumen. Oleh sebab itu, kami ingin memberikan informasi mengenai definisi dan cara menghitung menggunakan rumus uji t.

Teori dasar uji t
Seperti yang kita ketahui bahwa uji t dikenal sebagai uji parsial yang digunakan untuk menguji seperti apa pengaruh dari masing-masing variabel bebas secara terpisah (sendiri-sendiri) terhadap variabel terikat (dependent).
Uji ini juga dapat dilakukan dengan membandingkan antara nilai t hitung (berdasarkan hasil perhitungan) dengan t tabel (yang bisa diperoleh dari tabel statistik) dengan cara melihat kolom yang signifikan pada setiap t hitung.
Rumus uji t yang digunakan di laboratorium
Sebagai informasi atau sharing saja bahwa biasanya uji t digunakan untuk probabilitas linieritas data yang terikat. Adapun penggunaan lain yaitu menentukan kepada hasil, apakah pengukuran tersebut dapat dibandingkan secara statistik dengan nilai standar yang ada pada tabel ujit
Membandingkan nilai rata-rata
Sering kali pada saat melakukan evaluasi terhadap kegiatan validasi metode yakni dalam menentukan metode kandidat, kita melakukan pengujian yang berulang misalkan 7 kali. Nah, hal yang biasa kita bandingkan adalah nilai rata-rata dari pengulangan tersebut.
Melalui pembandingan tersebut kita dapat memberikan kesimpulan, apakah hasil dari analisis terhadap 2 metode berbeda tersebut masih setara atau berbeda signifikan? Nah, melalui uji t ini, kita akan mampu membuat keputusan tentang metode mana yang layak untuk digunakan oleh laboratorium saudara/i.
Cara Menghitung Uji t
Untuk dapat menghitung atau menganalisis suatu data, rumus uji t yang biasa kita gunakan di laboratorium adalah seperti pada gambar berikut ini:
Keterangan rumus:
X1 adalah nilai rata-rata pada kumpulan data pertama
X2 adalah nilai rata-rata dari kumpulan data kedua
N1 adalah jumlah ulangan atau data pada kumpulan data pertama
N2 adalah jumlah ulangan atau data pada sekumpulan data kedua
S adalah standar deviasi atau variansi
Nah, untuk menghitung S dapat menggunakan rumus berikut ini:
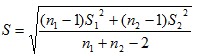
Keterangan dari rumus S tersebut adalah:
n1 adalah jumlah data atau ulangan pada kumpulan pertama
n2 adalah jumlah data atau ulangan pada kumpulan kedua
S1 adalah standar deviasi dari kumpulan data pertama
S2 adalah standar deviasi dari kumpulan data kedua
Contoh Perhitungan
Saya mengambil contoh perhitungan dari salah satu website ternama yaitu sampling-analisis.com yang memberikan contoh seperti ini:
Baca Juga: JAMINAN MUTU LABORATORIUM
Pada pengukuran 10 kali ulangan yang bertujuan untuk membandingkan 2 metode yakni metode lama dan metode baru (kandidat) diperoleh data seperti pada tabel berikut ini:

Berdasarkan hasil perhitungan menggunakan excel, diperoleh nilai rata-rata dari 10 ulangan tersebut adalah X1 = 17,66 (metode baru) dan X2 = 17,58 (metode lama). Secara kasat mata, tentunya kita akan kesulitan untuk membandingkan kedua kelompok data tersebut. Oleh sebab itu kita bisa menggunakan rumus uji t untuk menyelesaikannya.
Sebelum masuk ke rumus uji t, maka kita hitung terlebih dahulu nilai S1 dan S2 yang disajikan pada contoh di bawah ini:

Okay, setelah kita dapatkan nilai S1 dan S2 maka berikutnya adalah masukkan pada rumus seperti di bawah ini:

Ternyata setelah kita hitung, bahwa nilai S nya adalah 1,58, tahap selanjutnya silahkan masukkan ke rumus berikut ini:

Wah, sudah hampir selesai...
Ternyata nilai t hitungnya adalah 0,11 dan tahap terakhir adalah silahkan cek nilai t pada tabel berikut ini (tabel bisa dicari di internet, juga banyak kok)
Nilai derajat bebas untuk uji t adalah (n1 + n2) - 2, jadi nilainya adalah 10+10-2 = 18
Ok, berdasarkan dari tabel uji t pada tingkat kepercayaan 95%, diperoleh nilai t tabel adalah 1,734.
Semakin terlihat jelas bukan, apakah data berbeda signifikan atau tidak melalui data t hitung dan t tabel.
Karena t hitung < t tabel maka sekompulan data tidak berbeda secara signifikan.































